Neural Symbolic Weakly Supervised Semantic Parsing
Written by Evelyn(Yining) Hong
Department of Computer Science
Feb.10th, 2020
Literature Survey of CS269
Paper: Neural Symbolic Machines: Learning Semantic Parsers on Freebase with Weak Supervision
ACL 2017
Chen Liang, Jonathan Berant, Quoc Le, Kenneth D. Forbus, Ni Lao
What is Semantic Parsing?
The goal of semantic parsing is to generate compositional, executable, formal representation, e.g. code/sql/sparql.
Formal representation requires following strict constraints:
- Syntax (e.g., correct number of parentheses)
- Semantics (e.g., calling function with the right type of arguments)
Previously, most semantic parsing tasks make use of Seq2Seq model. It was first introduced into this area by (Dong & Lapata, 2016). With a single neural network, it soon beat all the other rule-based human-written semantic parsing techniques. The authors also propose seq2tree because semantic sentences always have hierarchical structure. Seq2seq structures are easy to build with toolkits.
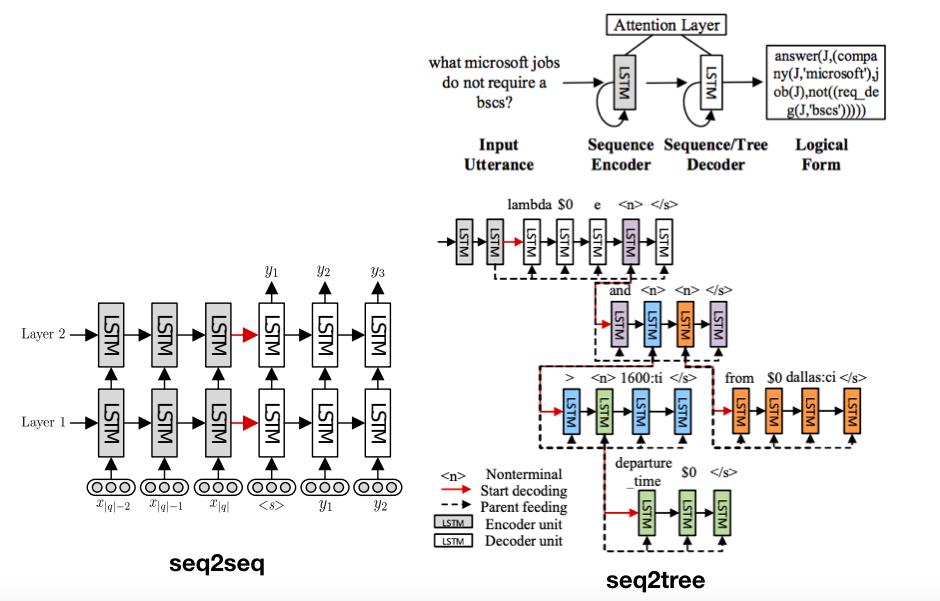
Neural Symbolic Weakly Supervised Semantic Parsing
Recently, the neural-symbolic paradigm has been extensively explored in the tasks of semantic parsing. Concretely, for these tasks, neural networks are used to map raw signals (images/questions/instructions) to symbolic representations (scenes/programs/actions), which are then used to perform symbolic reasoning/execution to generate final outputs. Weak supervision in these tasks usually provides pairs of raw inputs and final outputs, with intermediate symbolic representations unobserved.

Since symbolic reasoning is non-differentiable, previous methods usually learn the neural-symbolic models by policy gradient methods like REINFORCE. The policy gradient methods generate samples and update the policy based on the generated samples that happen to hit high cumulative rewards.
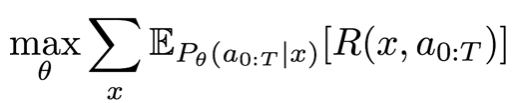
Neural Symbolic Machines
Back to our paper, “Neural Symbolic Machines: Learning Semantic Parsers on Freebase with Weak Supervision”.
Seq2seq has a good performance. However it also has several disadvantages:
- Require strong/full supervision. So it is only applied on domains with tiny schemas/vocabs and known semantic annotations.
- Lack of integration with the executor. As we said before, intermediate symbolic programs must be executed to get the final answer. In seq2seq, only after the whole program is written can any feedback be generated from the executor. However, usually the search space is large and there’s no way to search over the exponentially large hypothesis space given a large schema. So the entire burden is on the neural network.
The authors present a manager-programmer-computer framework, in which the generated programs are executed sequentially.
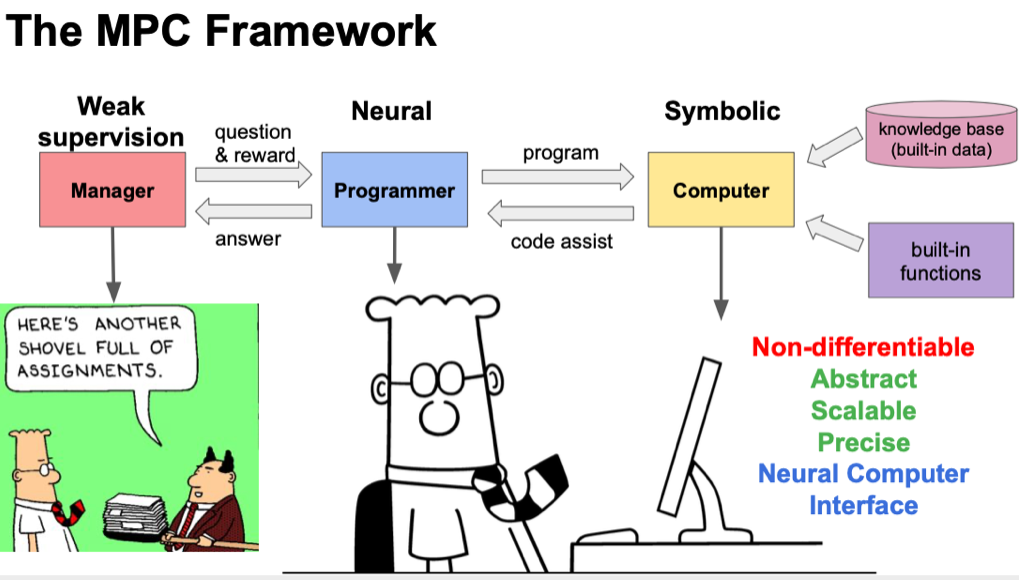
Dataset
They use the WebQuestions dataset. It contains 5810 questions crawled from Google Suggest API and answered using Amazon MTurk. Specifically, they have 3778 questions for training and 2032 for testing. A question may have multiple answers using Avg.F1 as main evaluation metric.
Symbolic Computer
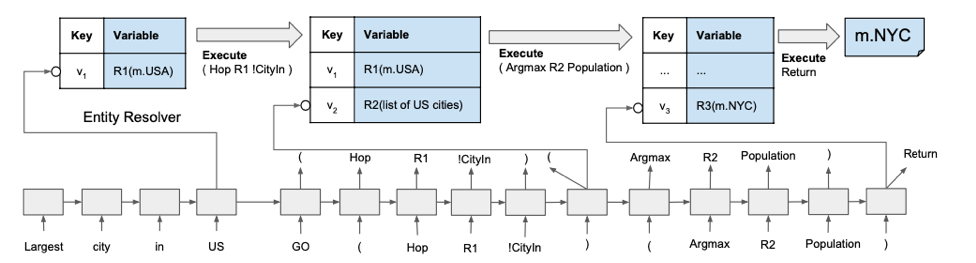
In fact, their computer -or symbolic part, is similar to Lisp, which is a high-level language with uniform syntax.
It’s composed of some predefined functions (F A0…Ak) where F is the function name and A0…Ak are variables (v) or relations (r).
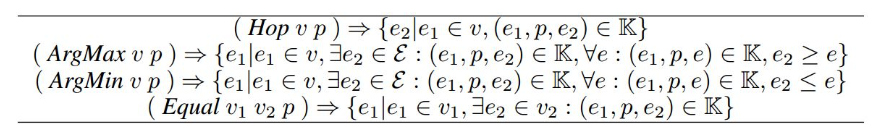
Seq2seq with Key-Variable Memory
They add a key-variable memory to seq2seq model for compositionality. The ‘keys’ are the outputs of GRUs. The ‘variables’ are just symbols referencing results in computer: ‘R1’, ‘R2’, and maybe used for the computer in the next stage.
Training with Iterative Maximum Likelihood & AUGMENTED REINFORCE
REINFORCE typically adopted by weakly-supervised reinforcement learning tasks suffer from several disadvantages:
- They experience “cold start”
- Training is slow and get stuck on local optimum. Converging slow.
- Search space is large. Rewards are sparse. Progarms that can generate correct answers only count for a small portion of all the programs.
THerefore, they train the model using augmented REINFORCE, in which they first do iterative maximum likelihood(ML) to find pseudo-gold programs with rewards 1. Train the ML part using this pesudo-gold programs as ground truth. Then they add this program to the REINFORCE beam, giving it with a relative large reward. The whole algorithm is presented below:

Their performance significantly outperforms others.
Related Works
There are many works focusing on addressing the REINFORCE problems mentioned above.
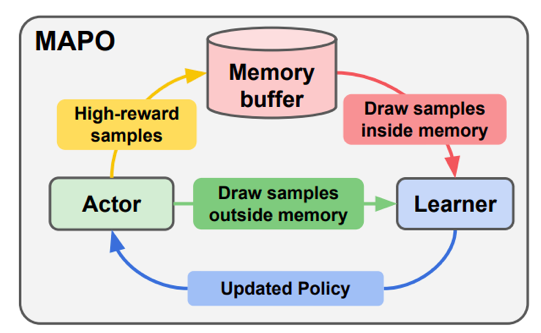
One is Memory Augmented Policy Optimization for Program Synthesis and Semantic Parsing They leverage a memory buffer of promising trajectories to reduce the variance of policy gradient estimate. They express the expected return objective as a weighted sum of two terms: an expectation over the high-reward trajectories inside the memory buffer, and a separate expectation over trajectories outside the buffer.
The other one aims to bridge the gap between Maximum Marginal Likelihood and Reinforcement Learning. The new algorithm guards against spurious programs by combining the systematic search traditionally employed in MML with the randomized exploration of RL, and by updating parameters such that probability is spread more evenly across consistent programs.
The Neural-Symbolic VQA and Neural-Symbolic Concept Learner are two papers that work on the VQA dataset CLEVR. Semantic parsing is also a crucial part of VQA. The questions are parsed into programs, which are then executed on the input images to get the answers. They use reinforcement learning to joinyly train the scene and semantic part.
Math word probelems are quite similar to semantic parsing. MathDQN: Solving Arithmetic Word Problems via Deep Reinforcement Learning is the first attempt to introduce deep reinforcement learning to solve arithmetic word problems. The motivation is that deep Q-network has witnessed success in solving various problems with big search space and achieves promising performance in terms of both accuracy and running time. So they design the states, actions, reward function, together with a feed-forward neural network as the deep Q-network and propose MathDQN.
Learning to Generalize from Sparse and Underspecified Rewards consider the problem of learning from sparse and underspecified rewards, where an agent receives a complex input, such as a natural language instruction, and needs to generate a complex response, such as an action sequence, while only receiving binary success-failure feedback. They address exploration by using a mode covering direction of KL divergence to collect a diverse set of successful trajectories, followed by a mode seeking KL divergence to train a robust policy.